Accuracy metrics provided by @UmpScorecards represent the proportion of taken pitches called correctly over a certain subset of taken pitches (a game, a season, etc.).
To determine if a pitch was called correctly, our algorithm starts by calculating the likelihood that the pitch was a strike. This is done using a Monte Carlo simulation of a pitch's potential true location, given its reported location and a distribution that represents potential measurement error (both vertical and horizontal) within the Hawkeye tracking system. For each pitch, 500 potential true locations are simulated, and the likelihood that a given pitch is a strike corresponds to the proportion of the pitch's simulated potential true locations that fall within the strike zone. To read about how we determine whether an individual pitch falls within the strike zone, and, more generally, how we determine the size of the strike zone, click here. To learn more about the Hawkeye measurement system and its potential biases, read here.
From there, we consider a taken pitch to be incorrectly called if one of two conditions hold: the probability that the pitch was truly a strike was over 90%, and the umpire called it a ball; the probability that the pitch was a ball was over 90%, and the umpire called it a strike.
The team at @UmpScorecards thinks that this method strikes a good balance between interpretability, validity, practicality, and fairness. Other methods, such as using a harsh cut off at the edge of the zone (what we did when this account was first created), or using a universal 1 inch margin of error past the strike zone, tend to sacrifice at least one of these.
Accuracy Above Expected (AAx) and related metrics — new as of v3.1.0 [7-21-2022]
Expected metrics provided by @UmpScorecards reflect how umpires perform in a game or across a season, relative to the expected performance from an average umpire.
Our expectation model starts by calculating the likelihood that any given pitch is called correctly (correct in this case refers to the @UmpScorecards methodology for determining correctness). We estimate correct call likelihood as a baseline likelihood plus a dynamic adjustment term to account for time-based changes in umpiring accuracy. The baseline likelihood comes from a multilayered perceptron neural network trained on a representative sample (so as to not give extra weight to certain umpires) of pitches thrown between 2015 and 2021. Inputs into this model include the pitch’s horizontal and vertical location, the pitch’s type (fastball, slider, etc.), the size and height of the strike zone, and other contextual factors such as the count and the handedness of the batter. Below is a calibration curve for our baseline correct call likelihood model; the predictions our model has made are broken into 20 buckets, and we've plotted our average prediction of each bucket against the true frequency of predictions in each bucket.
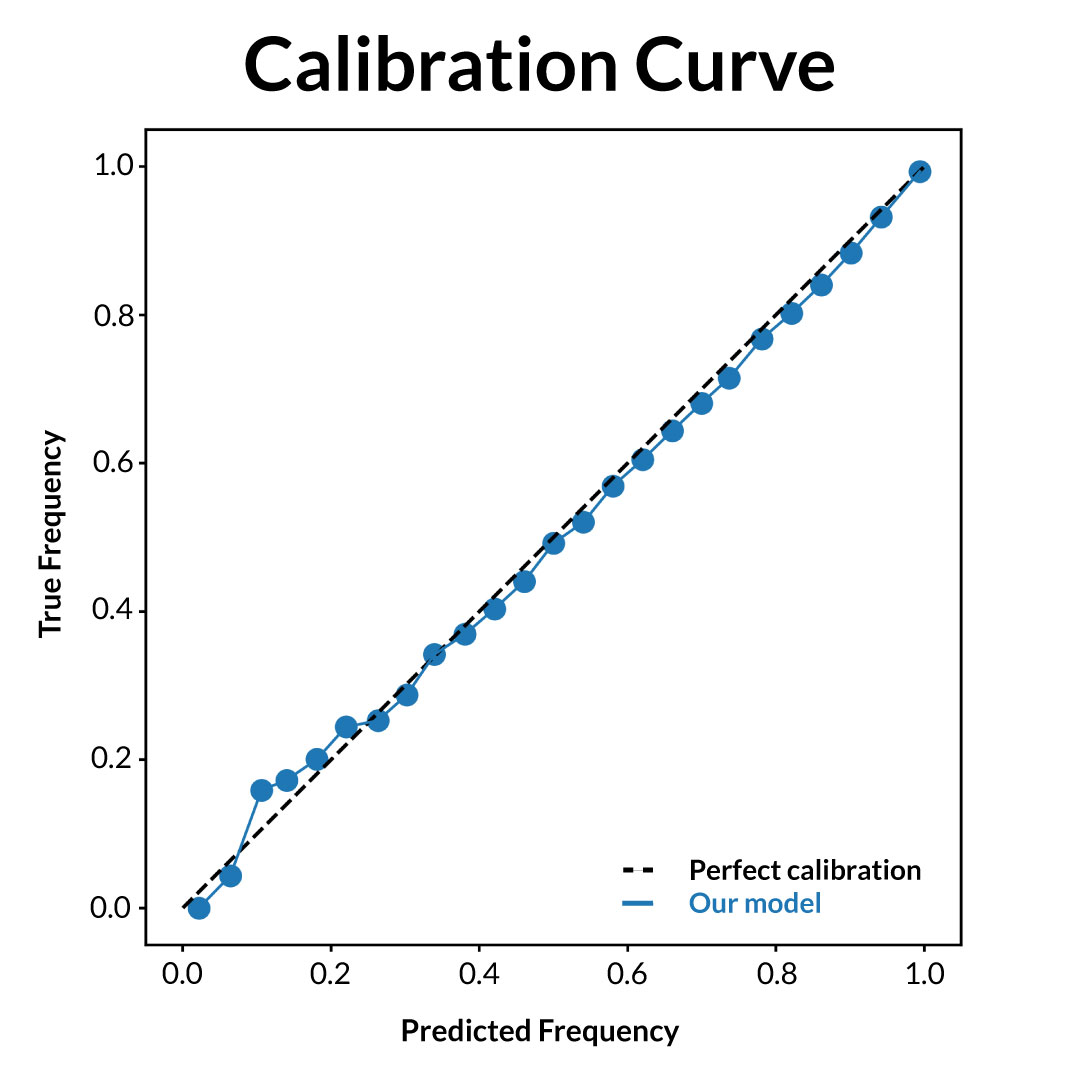
Our model is calibrated well, that is, events we estimate to have a likelihood of 𝑥 occur (roughly) 𝑥 percent of the time.
Our model results also confirm the theory that umpires have improved over time. Here is the same calibration curve, broken up by year.
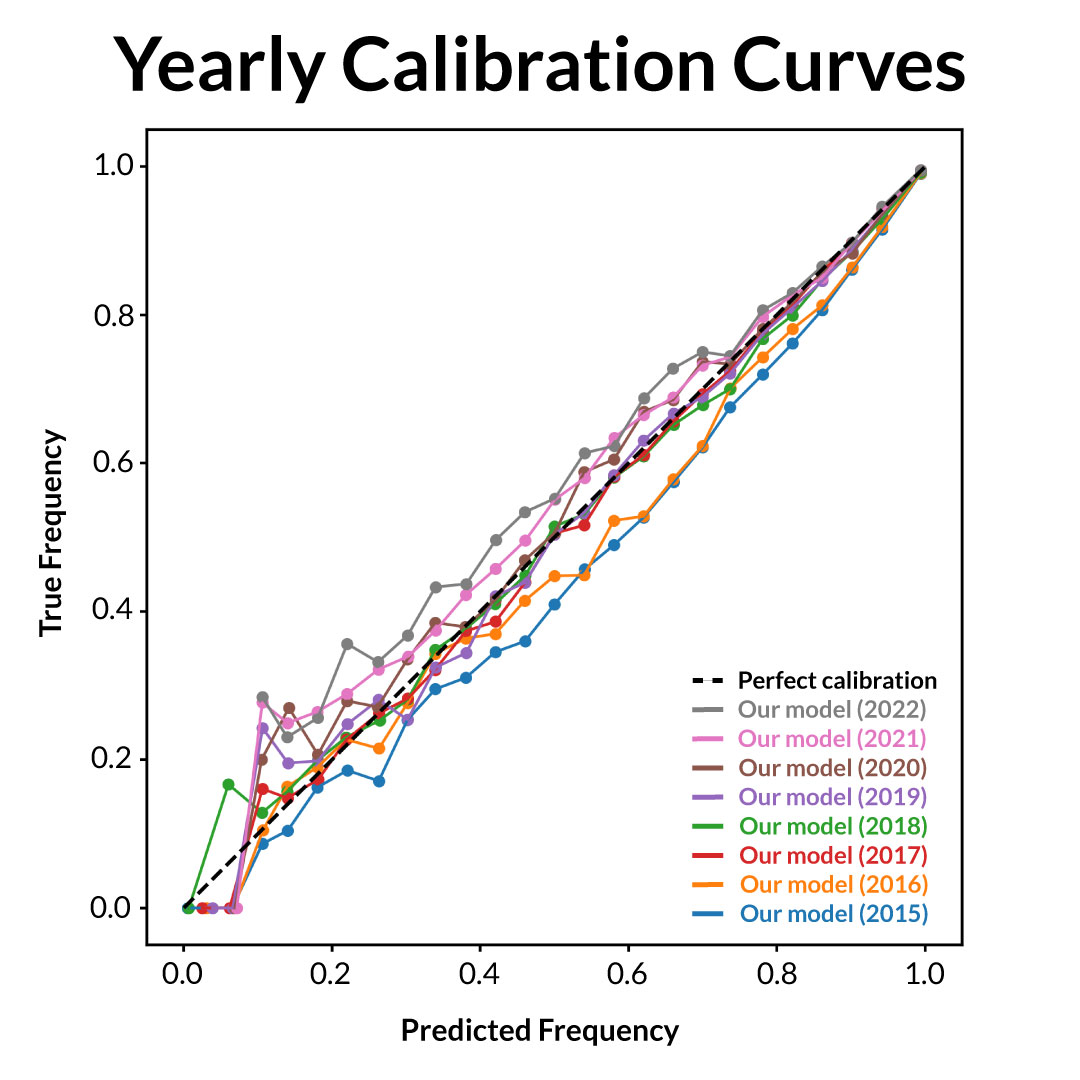
Our model is significantly under confident on umpires in 2022 (curve is above perfect calibration), and significantly over confident on umpires in 2015 (curve is below perfect calibration). To account for these significant season-to-season changes in umpire accuracy, we therefore added the adjustment term to the model.
Once we have an adjusted correct call likelihood for each pitch, we take the sum for each pitch across a game or season to calculate an expected number of correct calls, or an expected accuracy. This value can be compared with an umpire’s true number of correct calls to emphasize their performance relative to what was ‘expected’ of them.
In developing our model, we took inspiration from multiple sources, especially this article by Cameron Grove (@Pitching_bot on Twitter) and this article from Scott Spencer.
To determine if a pitch was called correctly, our algorithm starts by calculating the likelihood that the pitch was a strike. This is done using a Monte Carlo simulation of a pitch's potential true location, given its reported location and a distribution that represents potential measurement error (both vertical and horizontal) within the Hawkeye tracking system. For each pitch, 500 potential true locations are simulated, and the likelihood that a given pitch is a strike corresponds to the proportion of the pitch's simulated potential true locations that fall within the strike zone. To read about how we determine whether an individual pitch falls within the strike zone, and, more generally, how we determine the size of the strike zone, click here. To learn more about the Hawkeye measurement system and its potential biases, read here.
From there, we consider a taken pitch to be incorrectly called if one of two conditions hold: the probability that the pitch was truly a strike was over 90%, and the umpire called it a ball; the probability that the pitch was a ball was over 90%, and the umpire called it a strike.
The team at @UmpScorecards thinks that this method strikes a good balance between interpretability, validity, practicality, and fairness. Other methods, such as using a harsh cut off at the edge of the zone (what we did when this account was first created), or using a universal 1 inch margin of error past the strike zone, tend to sacrifice at least one of these.
Our expectation model starts by calculating the likelihood that any given pitch is called correctly (correct in this case refers to the @UmpScorecards methodology for determining correctness). We estimate correct call likelihood as a baseline likelihood plus a dynamic adjustment term to account for time-based changes in umpiring accuracy. The baseline likelihood comes from a multilayered perceptron neural network trained on a representative sample (so as to not give extra weight to certain umpires) of pitches thrown between 2015 and 2021. Inputs into this model include the pitch’s horizontal and vertical location, the pitch’s type (fastball, slider, etc.), the size and height of the strike zone, and other contextual factors such as the count and the handedness of the batter. Below is a calibration curve for our baseline correct call likelihood model; the predictions our model has made are broken into 20 buckets, and we've plotted our average prediction of each bucket against the true frequency of predictions in each bucket.

Our model results also confirm the theory that umpires have improved over time. Here is the same calibration curve, broken up by year.

Once we have an adjusted correct call likelihood for each pitch, we take the sum for each pitch across a game or season to calculate an expected number of correct calls, or an expected accuracy. This value can be compared with an umpire’s true number of correct calls to emphasize their performance relative to what was ‘expected’ of them.
In developing our model, we took inspiration from multiple sources, especially this article by Cameron Grove (@Pitching_bot on Twitter) and this article from Scott Spencer.